Technical documentation

Code walk-through

The project repository is composed of a main_nb script, a calib_nb script (a static version of which is shown in Notebook: run model and Notebook: run calibration), and plots scripts, themselves calling on several secondary scripts and custom packages. Those packages in turn include modules that are used at different steps of the code:

• inputs: contains the modules used to import default parameters and options, as well as pre-treated data.

• equilibrium: contains the modules used to compute the static equilibrium allocation, as well as the dynamic simulations.

• outputs: contains the modules used to visualize results and data.

• calibration: contains the modules used to re-run the calibration of parameters if necessary.

All the scripts placed at the root start with a preamble that imports (python and custom) packages to be used, and defines the file paths that integrate the repository to the local system of the user. They then go on calling the packages described above. They make almost all the same calls on the inputs package, then specific calls depending on the script (main_nb mostly draws on equilibrium, calib_nb on calibration, and plots scripts on outputs). Let us start describing those packages by following along the main_nb script (we refer the reader to API reference for detailed information on the functions we will use).

Inputs

Parameters and options

In this part, the code calls on the parameters_and_options.py module that imports the default parameters and options, then sets the timeline for the simulations, and overwrites the default parameters and options according to the specific scenario one is interested in. The detail of key parameters and options is given in Input tables (there are other technical parameters and options that should be of no interest for the end user) 1. Typically, one may set options allowing or not agents to anticipate floods, take climate climate change into account, or new informal settlements to be built.

Note that, on top of the import_options and import_param functions, the code later calls on a import_construction_parameters function that makes use of imported data to define additional parameter variables.

The key ones are the mini_lot_size parameter and the agricultural_rent variable (defined through compute_agricultural_rent as a function of other parameters). Here is how to interpret the value of agricultural rent. We assume that the price of agricultural land (corresponding to landlords’ outside options / opportunity cost, here agricultural_price_baseline parameter) is fixed and that agricultural land is undeveloped. Since we assume that developers make zero profit in equilibrium due to pure and perfect competition, this gives us a relation to obtain the minimum rent developers would be willing to accept if this land were urbanized 2:

\[R_A = \frac{(\delta P_A)^a (\rho + \delta)^{1-a}}{\kappa a^a (1-a)^{1-a}}\]

In the compute_agricultural_rent function, this corresponds to:

        agricultural_rent = (
            rent ** param["coeff_a"]
            * interest_rate ** param["coeff_a"]
            * (param["depreciation_rate"] + interest_rate) ** param["coeff_b"]
            / (scale_fact * param["coeff_b"] ** param["coeff_b"]
                * param["coeff_a"] ** param["coeff_a"])
            )

Below this rent, it is therefore never profitable to build housing. Agricultural rent defines a floor on equilibrium rent values as well as an endogenous city edge.

To store the output in a dedicated folder, we create a name associated to the parameters and options used. This name is a code associated to the options, parameters, and scenarios that we changed across our main simulation runs. They can be safely updated by the end user.

Assumptions

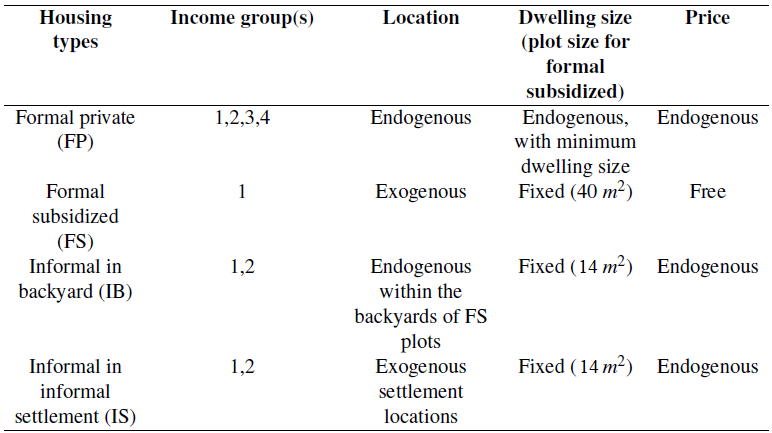
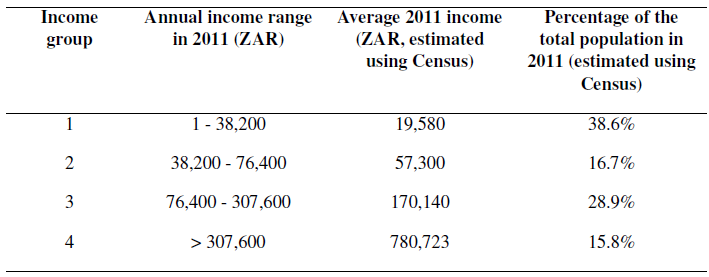
Note that, in the model, we consider three endogenous housing markets (whose allocation is computed in equilibrium) - namely, formal private housing, informal backyards (erected in the backyard of formal subsidized housing dwelling units), and informal settlements (in predetermined locations) 3 - one exogenous housing market (whose allocation is directly taken from the data) - the RDP (Reconstruction and Development Programme) formal subsidized housing 4 - and four income groups.

By default, only agents from the poorest income group have access to RDP housing units. Without loss of generality, we assume that the price of such dwellings is zero, and that they are allocated randomly to the fraction of poorest agents they can host, the rest being rationed out of the formal subsidized housing market. Then, the two poorest income groups sort across formal private housing, informal backyards, and informal settlements; whereas the two richest only choose to live in the formal private housing units. Those assumptions are passed into the code through the income_class_by_housing_type parameter. We believe that this is a good approximation of reality. Also note that, although the two richest income groups are identical in terms of housing options, we distinguish between them to better account for income heterogeneity and spatial sorting along income lines in our simulations, while keeping the model sufficiently simple to be solved numerically.

Modeling assumptions regarding housing (Source: Pfeiffer et al. [2019])

Data

Then, the code calls on the data.py module. This allows to import basic geographic data, macro data, households and income data, land use projections, flood data, scenarios for time-dependent variables, and transport data (see Setup for the appropriate tree structure where to locate the data folder). The databases used are presented in Data bases. A more detailed view on the specific data sets called in the code, and their position in the folder architecture, is given in Key data sets 5.

It should be noted that, by default, housing type data (used for validation) has already been converted from the SAL (Small Area Level) dimension to the grid dimension (500x500m pixels) with the import_sal_data and gen_small_areas_to_grid functions, and that income net of commuting costs for each income group and each grid cell (from transport data) has already been computed from the calibrated incomes for each income group and each job center with the import_transport_data function. If one wants to run the process again, one needs to overwrite the associated default options (please note that this may take some time to run). The import of flood data (through the import_full_floods_data function) is also a little time-consuming when agents are set to anticipate floods.

A bit counter-intuitively, the scenario for the interest rate does not only serve to define future values of the variable (more on that in Subsequent periods), but also its value at the initial state (as the raw data contains both past and future values). As part of the import_macro_data function, the interest_rate variable is defined as an average over the past three years, through the interpolate_interest_rate function defined in the functions_dynamic.py module (included in the equilibrium package). This allows to smooth outcomes around a supposed equilibrium value:

    #  Import interest rate history + scenario until 2040
    scenario_interest_rate = pd.read_csv(
        path_scenarios + 'Scenario_interest_rate_1.csv', sep=';')
    #  Fit linear regression spline centered around baseline year
    spline_interest_rate = interp1d(
        scenario_interest_rate.Year_interest_rate[
            ~np.isnan(scenario_interest_rate.real_interest_rate)]
        - param["baseline_year"],
        scenario_interest_rate.real_interest_rate[
            ~np.isnan(scenario_interest_rate.real_interest_rate)],
        'linear'
        )
    #  Get interest rate as the mean (in %) over (3) last years
    interest_rate = eqdyn.interpolate_interest_rate(spline_interest_rate, 0)

def interpolate_interest_rate(spline_interest_rate, t):
    """
    Return real interest rate used in model, for a given year.

    Parameters
    ----------
    spline_interest_rate : interp1d
        Linear interpolation for the interest rate (in %) over the years
    t : int
        Year for which we want to run the function

    Returns
    -------
    float64
        Real interest rate used in the model, and defined as the average over
        past (3) years to convey the structural (as opposed to conjonctural)
        component of the interest rate

    """
    nb_years = 3
    interest_rate_n_years = spline_interest_rate(np.arange(t - nb_years, t))
    interest_rate_n_years[interest_rate_n_years < 0] = np.nan
    return np.nanmean(interest_rate_n_years)/100

The imported files can be modified directly in the data repository, to account for changes in scenarios for instance, as long as the format used remains the same (see API reference for more details on each function requirements). Before going to the next step of the code, we would like to give more details on the imports of land use, flood, and transport data, which we think are not as transparent as the rest of the imports.

Land use data

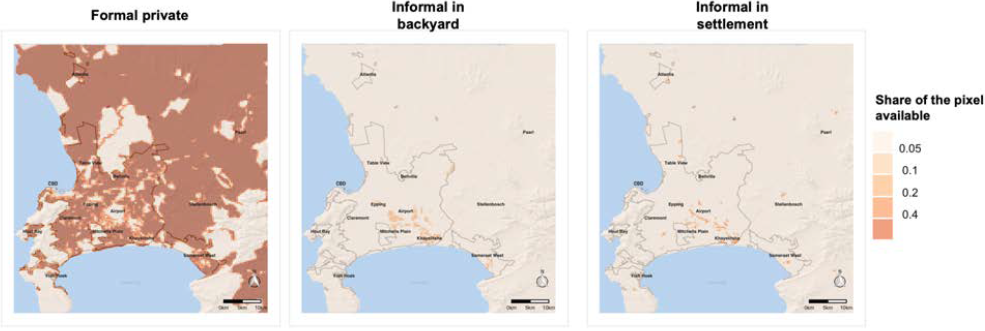
The import_land_use and import_coeff_land functions define exogenous land availability \(L^h(x)\) for each housing type \(h\) and each grid cell \(x\). Indeed, we assume that different kinds of housing do not get built in the same places to account for insecure property rights (in the case of informal settlements vs. formal private housing) and housing specificities (in the case of non-market formal subsidized housing and informal backyards located in the same premises) 6. Furthermore, \(L\) varies with \(x\) to account for both natural and regulatory constraints, infrastructure and other non-residential uses.

As \(L^h(x)\) is going to vary across time periods, the first part of the import_land_use function imports estimates for historical and projected land uses. It then defines linear regression splines over time for a set of variables, the key ones being the share of pixel area available for formal subsidized housing, informal backyards, informal settlements, and unconstrained development. Note that, in our benchmark (allowing for informal settlement expansion), land availability for informal settlements is defined over time by the intersection between the timing map below and the high and very high probability areas (also defined below).

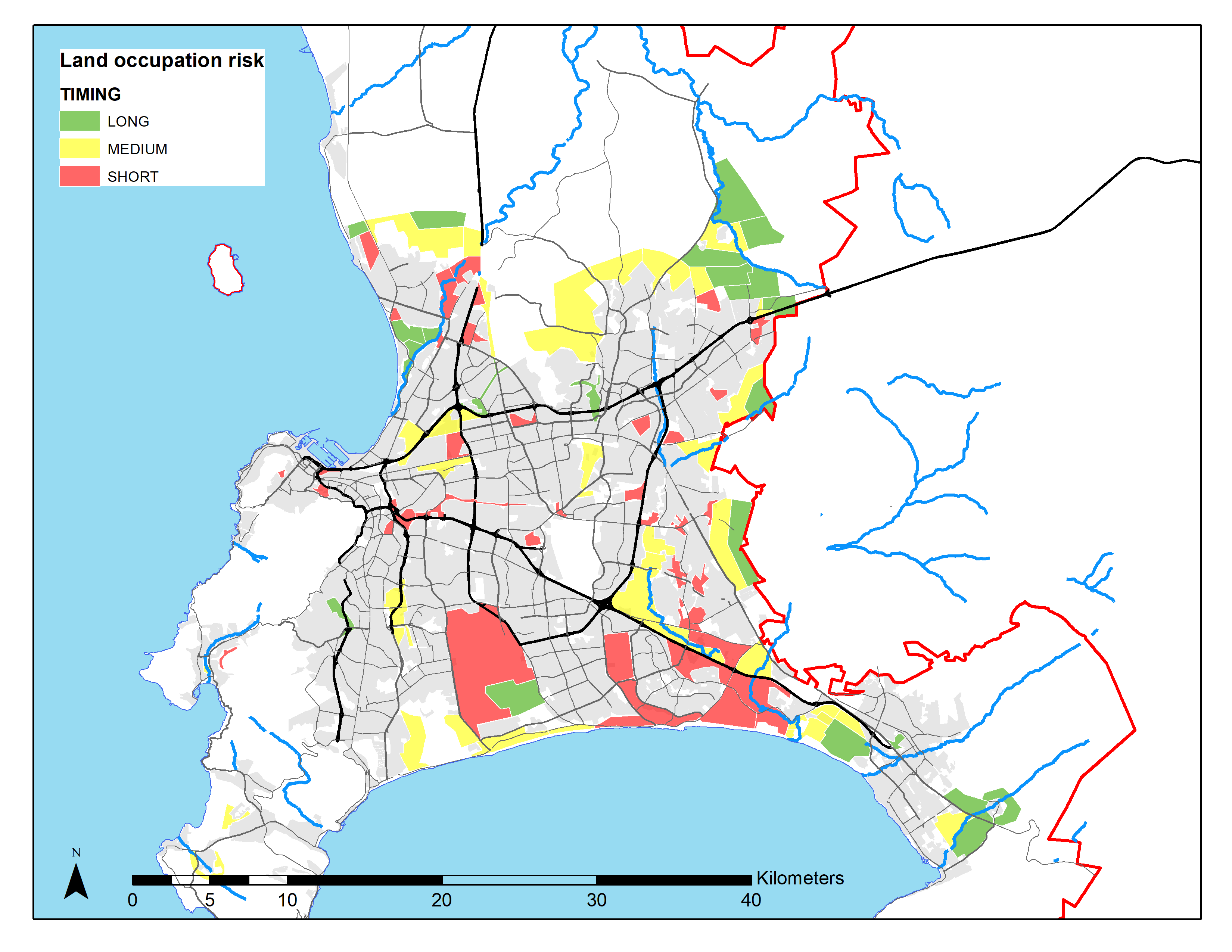
Estimated timing of future new informal settlements (Source: expert estimates)

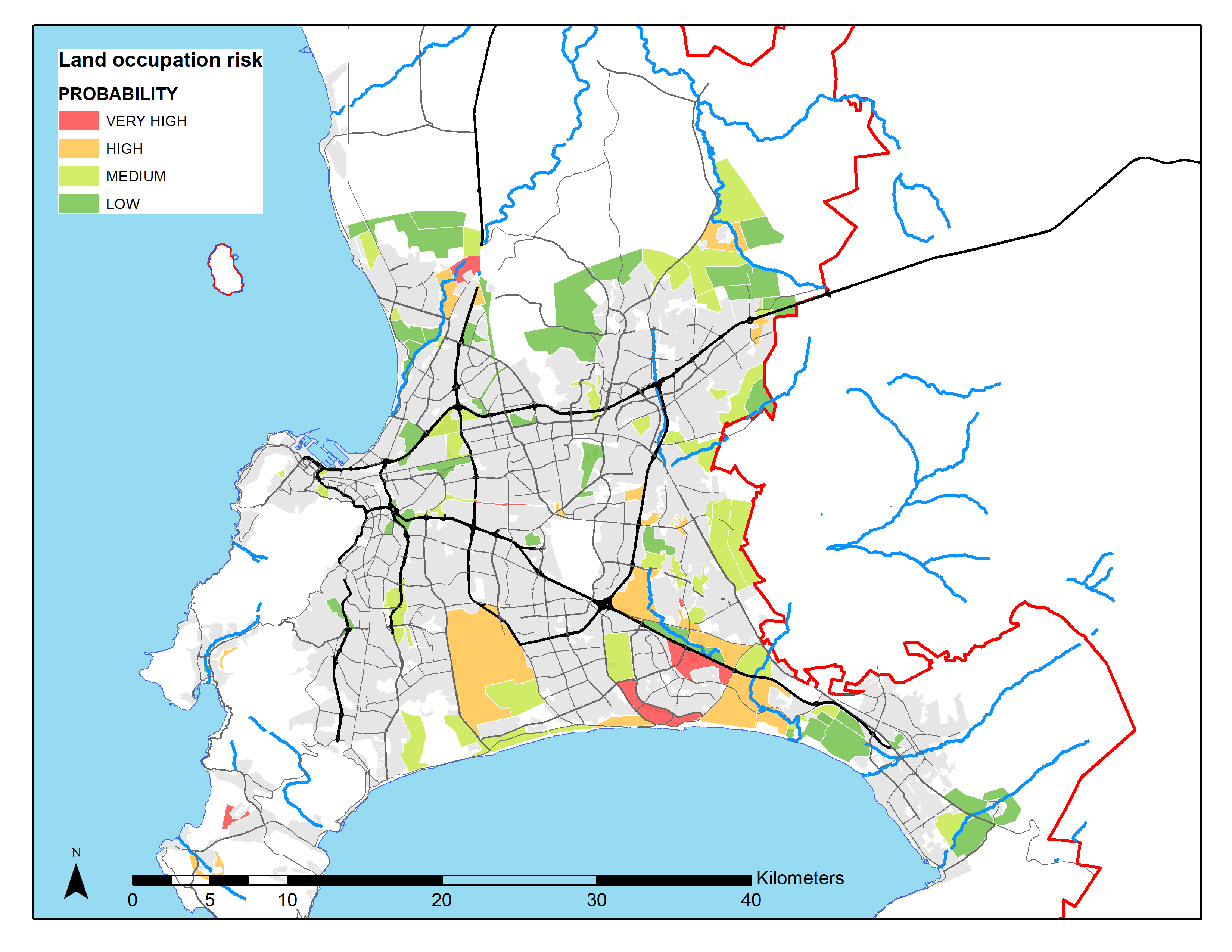
Estimated probability of future new informal settlements (Source: expert estimates)

The import_coeff_land function then takes those outputs as arguments and reweight them by a housing-specific maximum land-use parameter. This parameter allows to reduce the development potential of each area to its housing component (accounting for roads, for instance). The share of pixel area available for formal private housing (in a given period) is simply defined as the share of pixel area available for unconstrained development, minus the shares dedicated to the other housing types, times its own maximum land use parameter:

    coeff_land_private = (spline_land_constraints(t)
                          - spline_land_backyard(t)
                          - spline_land_informal(t)
                          - spline_land_RDP(t)) * param["max_land_use"]
    coeff_land_private[coeff_land_private < 0] = 0

    coeff_land_backyard = (spline_land_backyard(t)
                           * param["max_land_use_backyard"])
    coeff_land_RDP = spline_land_RDP(t) * param["max_land_use"]
    coeff_land_settlement = (spline_land_informal(t)
                             * param["max_land_use_settlement"])

The outputs are stored in a coeff_land matrix that yields the values of \(L^h(x)\) for each time period when multiplied by the area of a pixel. Results are shown in the figure below.

Share of available land for each housing type (Source: Pfeiffer et al. [2019])

Flood data

Flood data is processed through the import_init_floods_data, compute_fraction_capital_destroyed, and import_full_floods_data functions.

The import_init_floods_data function imports the pre-processed flood maps from FATHOM [Sampson et al., 2015] for fluvial and pluvial risks, and DELTARES [Deltares, 2021] for coastal risks. Those maps yield for each grid cell an estimate of the pixel share that is exposed to a flood of some maximum depth level, reached in a given year with a probability equal to the inverse of their return period. For instance, a flood map corresponding to a return period of 100 years considers events that have a 1/100 chance of occurring in any given year.

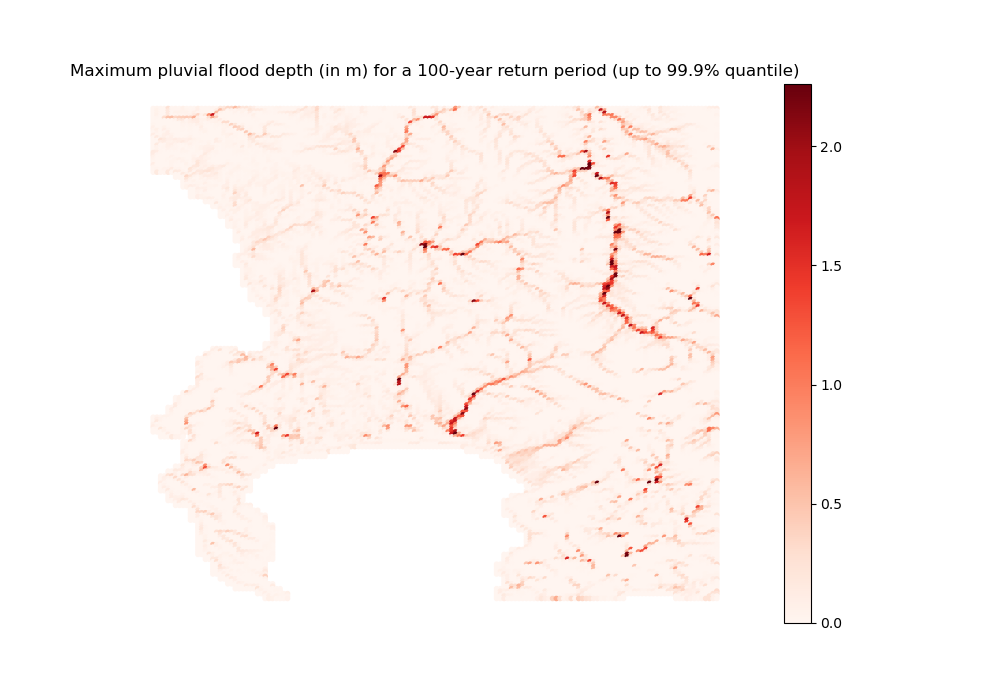
Maximum pluvial flood depth (in meters) for a 100-year return period (Source: FATHOM)

Note that the return periods considered are not the same for FATHOM and DELTARES data, and that different flood maps are available depending on the digital elevation model (DEM) considered, whether we account for sea-level rise, and whether we account for defensive infrastructure with respect to fluvial floods 7.

The function then imports depth-damage estimates from the existing literature. Those estimates, used in the insurance market, link levels of maximum flood depth to fractions of capital destroyed, depending on the materials affected by floods 8. More specifically, we use estimates from Englhardt et al. [2019] for damages to housing structures (depending on housing type), and from de Villiers et al. [2007] for damages to housing contents.

On this basis, the compute_fraction_capital_destroyed function integrates flood damages over the full range of return periods, for each flood type and damage function 9. This yields an annualized fraction of capital destroyed, corresponding to its expected value in a given year 10.

Finally, the import_full_floods_data function uses those outputs to define the depreciation term \(\rho_{h}^{d}(x)\) that is specific to housing type \(h\), damage type (structures or contents) \(d\), and location \(x\) (stored in the fraction_capital_destroyed matrix), by taking the maximum across fractions of capital destroyed for all flood types considered (a conservative assumption). When multiplied by some capital value, this term yields the expected economic cost from flood risks that is considered by anticipating agents when solving for equilibrium. It is also equal to the risk premium in the case of a perfect risk-based insurance market (leading to full insurance with actuarially fair prices) 11.

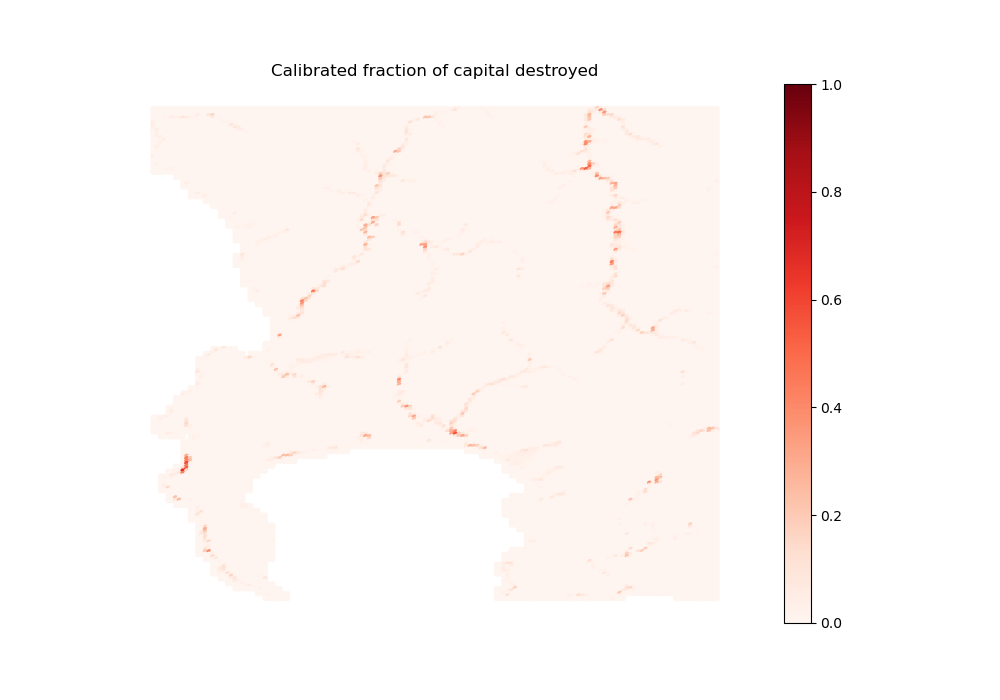
Annualized fraction of capital destroyed for structures in informal settlements

Transport data

Transport data is processed through the import_transport_data function. It imports monetary and time transport costs, and pre-calibrated incomes (income_centers_init parameter) per income group and job center (more on that in Transport costs), for a given dimension (grid-cell level or Small Place level) and a given simulation year (zero at initial state):

    # Import (monetary and time) transport costs
    (timeOutput, distanceOutput, monetaryCost, costTime
     ) = calcmp.import_transport_costs(
         grid, param, yearTraffic, households_per_income_class,
         spline_inflation, spline_fuel, spline_population_income_distribution,
         spline_income_distribution, path_precalc_inp, path_precalc_transp,
         dim, options)

    # Update average income and number of households per income group
    # for considered year
    incomeGroup, households_per_income_class = eqdyn.compute_average_income(
        spline_population_income_distribution, spline_income_distribution,
        param, yearTraffic)

    # We import expected income associated with each income center and income
    # group (from calibration)
    if options["load_precal_param"] == 1:
        income_centers_init = scipy.io.loadmat(
            path_precalc_inp + 'incomeCentersKeep.mat')['incomeCentersKeep']
    elif options["load_precal_param"] == 0:
        income_centers_init = np.load(
            path_precalc_inp + 'incomeCentersKeep.npy')
    # income_centers_init[income_centers_init == -np.inf] = np.nan

    # We correct the level of incomes per job center when overall average
    # income per income group changes with time (only used as an initial
    # value for the algorithm)
    incomeCenters = income_centers_init * incomeGroup / average_income

From there, it computes several outputs, of which the key variable is the expected income net of commuting costs \(\tilde{y}_i(x)\), earned by a household of income group \(i\) choosing to live in \(x\) (stored in the income_net_of_commuting_costs matrix). It is obtained by recursively solving for the optimal transport mode choice and job center choice of households characterized by \(i\) and \(x\) (see Commuting choice model for more details).

Equilibrium

This part of the main_nb script simply calls on two functions that return the key outputs of the model: compute_equilibrium solves the static equilibrium for baseline year, and run_simulation solves its dynamic version for all pre-defined subsequent years. Those functions in turn call on modules in the sub directory.

Initial state

Let us first dig into the compute_equilibrium function. Our main input is the total population per income group in the city at baseline year (2011). Since we took the non-employed (earning no income over the year) out to define our four income groups (with the inputs.data.import_income_classes_data function), we need to reweight total population to account for the overall number of households 12:

        ratio = population / sum(households_per_income_class)
        households_per_income_class = households_per_income_class * ratio

The associated distribution is given below:

Income groups used in the simulation (Source: Pfeiffer et al. [2019])

Then, considering that all formal subsidized housing belongs to the poorest income group, we substract the corresponding number of households from this class to keep only the ones whose allocation in the housing market is going to be determined endogenously:

    households_per_income_class[0] = np.max(
        households_per_income_class[0] - total_RDP, 0)

Finally, we shorten the grid to consider only habitable pixels (according to land availability and expected income net of commuting costs) to reduce numeric computations, and initialize a few key variables before starting the optimization per se:

    #  We select pixels with constructible shares for all housing types > 0.01
    #  and a positive maximum income net of commuting costs across classes
    #  NB: we will have no output in other pixels (numeric simplification)
    selected_pixels = (
        (np.sum(coeff_land, 0) > 0.01).squeeze()
        & (np.nanmax(income_net_of_commuting_costs, 0) > 0)
        )

Solving for equilibrium

Note that, among those variables, we define arbitrary values for utility levels across income groups:

    #  We take arbitrary utility levels, not too far from what we would expect,
    #  to make computation quicker
    utility[0, :] = np.array([1200, 4800, 16000, 77000])

This relates to the way this class of models is solved: as a closed-city equilibrium model, NEDUM-2D takes total population (across income groups) as exogenous, and utility levels (across income groups) as endogenous 13.

It is then solved iteratively in four steps:

• We first derive housing demand for each housing type

• We deduce rents for each housing type

• We then compute housing supply for each housing type

• From there, we obtain population in all locations for all housing types.

We update initial utility levels depending on the gap between the target and simulated population, and re-iterate the process until we reach a satisfying error level 14, according to the values of the parameters precision and max_iter. Of course, the closer the initial guess is to the final values, the quicker the algorithm converges. We will see below how each of the intermediate steps is computed.

A last word on the choice of a closed vs. open-city model: within a static framework, it is generally considered that closed-city models are a better representation of short-term outcomes and open-city models of long-term outcomes, as population takes time to adjust through migration. Here, we rely on scenarios from the CoCT (informed by more macro parameters than open-city models usually are) to adjust total population across time periods. Sticking to the closed-city model in those circumstances allows us to make welfare assessments based on utility changes without renouncing to the possibility that migrations occur.

Functional assumptions

Then, the compute_equilibrium function calls on the compute_outputs function for each endogenous housing type, which in turn calls on functions defined as part of the functions_solver.py module. This module applies formulas derived from the optimization process described in Pfeiffer et al. [2019].

Let us just rephrase the main assumptions here (refer to the paper for a discussion on those 15). The parameters highlighted in green are specific to a model with agents that perfectly anticipate flood risks.

On the one hand, households maximize Stone-Geary preferences:

\[U(z,q,x,h) = z^\alpha (q-q_0)^{1-\alpha}A(x)B^h(x)\]

• \(z\) is the quantity of composite good consumed (in monetary terms) and \(q\) is the quantity of housing consumed (in m²). They are the choice variables 16.

• \(x\) is the location where the household lives and \(h\) is the housing type considered. They are the state variables.

• \(\alpha\) is the composite good elasticity (alpha parameter), \(1 - \alpha\) is the surplus housing elasticity, and \(q_0\) (q0 parameter) is the basic need in housing.

• \(A(x)\) is a (centered around one) location-specific amenity index (precalculated_amenities parameter) and \(B^h(x)\) is a (positive) location-specific disamenity index equal to one in formal sectors and smaller than one in informal sectors (pockets and backyard_pockets parameters), to account for the negative externalities associated with living in such housing (such as eviction probability, etc.) 17. They are (calibrated) parameters.

They are facing the following budget constraint (optimization under constraint):

\[\tilde{y}_i(x) + \mathbb{1}_{h=FS} \mu(x)YR_{IB}(x) = (1 + \textcolor{green}{\gamma \rho_{h}^{contents}(x)})z + q_{h}R_{h}(x) + \mathbb{1}_{h \neq FP} (\rho + \textcolor{green}{\rho_{h}^{struct}(x)} + \mathbb{1}_{h \neq FS} \delta)v_{h}\]

• \(\tilde{y}_i(x)\) is the expected income net of commuting costs for a household of income group \(i\) living in location \(x\).

• \(\mathbb{1}_{h=FS}\) is an indicator variable for living in the formal subsidized housing sector. Indeed, such households have the possibility to rent out an endogenous fraction \(\mu(x)\) of their backyard of fixed size \(Y\) (backyard_size parameter) at the endogenous market rent \(R_{IB}(x)\).

• \(\textcolor{green}{\gamma}\) is the fraction of composite good exposed to floods (fraction_z_dwellings parameter) and \(\textcolor{green}{\rho_{h}^{contents}(x)}\) is the fraction of contents capital destroyed (that is location and housing-type specific): households need to pay for damages to their belongings.

• \(q_{h}\) is the (housing-type specific) amount of housing consumed, at the endogenous annual rent \(R_{h}(x)\).

• \(\mathbb{1}_{h \neq FP}\) is an indicator variable for living in a sector different from the formal private one. Indeed, such households (assimilated to owner-occupiers, more on that below) need to pay for the maintenance of their housing of capital value \(v_{h}\) (subsidized_structure_value and informal_structure_value parameters) that depreciate at rate \(\rho + \textcolor{green}{\rho_{h}^{struct}(x)}\) (depreciation_rate parameter + fraction_capital_destroyed matrix).

• \(\mathbb{1}_{h \neq FS}\) is an indicator variable for living in a sector different from the formal subidized one. Indeed, among the set of households described above, those who live in the informal sector (either backyards or settlements) also need to pay for the construction of their “shack” of capital value \(v_{h}\) 18. To do so, they pay a fraction of capital value \(\delta\) (interest_rate variable) of this price each year, which corresponds to the interest paid on an infinite debt (which is a good-enough approximation in a static setting).

On the other hand, formal private developers have a Cobb-Douglas housing production function expressed as:

\[s_{FP}(k) = \kappa k^{1-a}\]

• \(s_{FP}\) is the housing supply per unit of available land (in m² per km²).

• \(\kappa\) is a (calibrated) scale factor (coeff_A parameter).

• \(k = \frac{K}{L_{FP}}\) is the (endogenous) amount of capital per unit of available land (in monetary terms).

• \(a\) is the (calibrated) land elasticity of housing production (coeff_a parameter).

They therefore maximize a profit function (per unit of available land) defined as:

\[\Pi(x,k) = R_{FP}(x)s_{FP}(k) - (\rho + \textcolor{green}{\rho_{FP}^{struct}(x)} + \delta)k - \delta P(x)\]

• \(R^{FP}(x)\) is the (endogenous) market rent for formal private housing.

• \(P(x)\) is the (endogenous) price of land.

• \(k\) is the choice variable and \(x\) is the state variable.

Underlying those functional forms are structural assumptions about the maximization objective of agents on the supply and demand sides of each housing submarket:

• In the formal private sector, developers buy land from absentee landlords and buy capital to build housing on this land 19. They then rent out the housing at the equilibrium rent over an infinite horizon 20. They therefore internalize the costs associated with capital depreciation (both general and from structural flood damages) and interest rate (at which future flows of money are discounted). Households just have to pay for damages done to the content of their home 21.

• In the formal subsidized sector, (poor) households rent / buy housing for free from the State (owner-occupiers). They only pay for overall capital depreciation (general and from structural and content damages), and may rent out a fraction of their backyard.

• In the informal backyard sector, households rent a fraction of backyard (not directly housing) owned by formal subsidized housing residents and are responsible for building their own “shack” (owner-occupiers). Then, they pay for overall capital depreciation (general and from structural and content damages) and interest over construction costs too.

• In the informal settlement sector, households rent land from absentee landlords (not directly housing) and are responsible for building their own “shack” (owner-occupiers). Then, they pay for overall capital depreciation (general and from structural and content damages) and interest over construction costs too.

Note that both optimization programmes are concave, hence they can be maximized using first-order optimality conditions (setting the partial derivatives to zero), as detailed in Pfeiffer et al. [2019].

Equilibrium dwelling size

As announced in the Solving for equilibrium subsection, the compute_outputs function starts by computing housing demand / dwelling size (in m²) for each housing type through the compute_dwelling_size_formal function. Optimization over the households’ programme described above implicitly defines this quantity in the formal private sector:

\[u = (\frac{\alpha \tilde{y}_i(x)}{1 + \textcolor{green}{\gamma \rho_{FP}^{contents}(x)}})^\alpha \frac{Q^*-q_0}{(Q^* - \alpha q_0)^\alpha} A(x)\]

• \(u\) is the fixed utility level

• \(Q*\) is the equilibrium dwelling size

By reorganizing the above equation, we obtain the following left and right sides in the code:

    left_side = (
        (np.array(utility)[:, None] / np.array(amenities)[None, :])
        * ((1 + (param["fraction_z_dwellings"]
                 * np.array(fraction_capital_destroyed.contents_formal)[
                     None, :])) ** (param["alpha"]))
        / ((param["alpha"] * income_temp) ** param["alpha"])
        )

    result = (
        (q - q_0)
        / ((q - (alpha * q_0)) ** alpha)
        )

The compute_dwelling_size_formal function then recovers the value of \(Q*\) (depending on income group) through a linear interpolation, before constraining it to be larger than the parametrized minimum dwelling size in this sector (mini_lot_size parameter):

    f = interp1d(explicit_qfunc(x, param["q0"], param["alpha"]), x)

    # We define dwelling size as the image corresponding to observed values
    # from left_side, for each selected pixel and each income group
    dwelling_size = f(left_side)

    # We cap dwelling size to 10**12 (to avoid numerical difficulties with
    # infinite numbers)
    dwelling_size[dwelling_size > np.nanmax(x)] = np.nanmax(x)

Back to the compute_outputs function, the dwelling size in informal backyards and informal settlements is exogenously set as being the standard parametrized size of a “shack” (shack_size parameter).

Equilibrium rent

Plugging this back into the first-order optimality condition for formal private households, and just inverting the households’ programme for informal backyards and settlements, we obtain the following bid rents in each sector, depending on income group:

\[\Psi_i^{FP}(x,u) = \frac{(1-\alpha)\tilde{y}_i(x)}{Q_{FP}(x,i,u) - \alpha q_0}\]

• \(Q_{FP}(x,i,u) = max(q_{min},Q^*)\)

\[\Psi_i^{IB}(x,u) = \frac{1}{q_I}[\tilde{y}_i(x) - (\rho + \delta + \textcolor{green}{\rho_{IB}^{struct}})v_I - (1 + \textcolor{green}{\gamma \rho_{IB}^{contents}})(\frac{u}{(q_I-q_0)^{1-\alpha}A(x)B_{IB}(x)})^\frac{1}{\alpha}]\]

\[\Psi_i^{IS}(x,u) = \frac{1}{q_I}[\tilde{y}_i(x) - (\rho + \delta + \textcolor{green}{\rho_{IS}^{struct}})v_I - (1 + \textcolor{green}{\gamma \rho_{IS}^{contents}})(\frac{u}{(q_I-q_0)^{1-\alpha}A(x)B_{IS}(x)})^\frac{1}{\alpha}]\]

In the compute_outputs function, this corresponds to:

        R_mat = (param["beta"] * (income_net_of_commuting_costs)
                 / (dwelling_size - (param["alpha"] * param["q0"])))

            R_mat = (
                (1 / param["shack_size"])
                * (income_net_of_commuting_costs
                    - ((1 + np.array(
                        fraction_capital_destroyed.contents_backyard)[None, :]
                        * param["fraction_z_dwellings"])
                        * ((utility[:, None]
                            / (amenities[None, :]
                               * param_backyards_pockets[None, :]
                               * ((dwelling_size - param["q0"])
                                  ** param["beta"])))
                           ** (1 / param["alpha"])))
                    - (param["informal_structure_value"]
                       * (interest_rate + param["depreciation_rate"]))
                    - (np.array(
                        fraction_capital_destroyed.structure_informal_backyards
                        )[None, :] * param["informal_structure_value"]))
                )

        R_mat = (
            (1 / param["shack_size"])
            * (income_net_of_commuting_costs
                - ((1 + np.array(fraction_capital_destroyed.contents_informal)[
                    None, :] * param["fraction_z_dwellings"])
                    * ((utility[:, None] / (amenities[None, :]
                                            * param_pockets[None, :]
                                            * ((dwelling_size - param["q0"])
                                               ** param["beta"])))
                       ** (1 / param["alpha"])))
                - (param["informal_structure_value"]
                   * (interest_rate + param["depreciation_rate"]))
                - (np.array(
                    fraction_capital_destroyed.structure_informal_settlements
                    )[None, :] * param["informal_structure_value"]))
            )

Bid rents \(\Psi^i_h(x,u)\) correspond to the maximum amount households of type \(i\) are willing to pay for a unit (1 m²) of housing of type \(h\) in a certain location \(x\) for a given utility level \(u\) (over one year). Assuming that households bid their true valuation and that there are no strategic interactions, housing / land 22 is allocated to the highest bidder. This is why we retain the bid rents from the highest bidding income groups, and the associated dwelling sizes, as the equilibrium output values for rents and dwelling sizes. In the code, this corresponds to:

    # We select highest bidder (income group) in each location
    proba = (R_mat == np.nanmax(R_mat, 0))
    # We correct the matrix if binding budget constraint
    # (and other precautions)
    limit = ((income_net_of_commuting_costs > 0)
             & (proba > 0)
             & (~np.isnan(income_net_of_commuting_costs))
             & (R_mat > 0))
    proba = proba * limit

    # Yields directly the selected income group for each location
    which_group = np.nanargmax(R_mat, 0)

    # Then we recover rent and dwelling size associated with the selected
    # income group in each location
    R = np.empty(len(which_group))
    R[:] = np.nan
    dwelling_size_temp = np.empty(len(which_group))
    dwelling_size_temp[:] = np.nan
    for i in range(0, len(which_group)):
        R[i] = R_mat[int(which_group[i]), i]
        dwelling_size_temp[i] = dwelling_size[int(which_group[i]), i]

Equilibrium housing supply

Then, the compute_outputs function goes on calling the compute_housing_supply_formal and compute_housing_supply_backyard functions.

In the formal private sector, profit maximization of developers with respect to capital yields:

\[s_{FP}(x) = \kappa^{\frac{1}{a}} (\frac{(1-a)R_{FP}(x)}{\rho + \textcolor{green}{\rho_{FP}^{struct}(x)} + \delta})^{\frac{1-a}{a}}\]

In the code, this corresponds to:

        # NB: we convert values to supply in m² per km² of available land
        housing_supply = (
            1000000
            * (construction_param ** (1/param["coeff_a"]))
            * ((param["coeff_b"]
                / (interest_rate + param["depreciation_rate"]
                   + capital_destroyed))
               ** (param["coeff_b"]/param["coeff_a"]))
            * ((R) ** (param["coeff_b"]/param["coeff_a"]))
            )

In the informal backyard sector, utility maximization of households living in formal subsidized housing with respect to fraction of backyard rented out yields:

\[\mu(x) = \alpha \frac{q_{FS}-q_0}{Y} - (1-\alpha) \frac{\tilde{y}_1(x) - (\rho + \textcolor{green}{\rho_{FS}^{struct}(x)}) \textcolor{green}{h_{FS}}}{YR_{IB}(x)}\]

In the code, this corresponds to:

    housing_supply = (
        (param["alpha"] *
         (param["RDP_size"] + param["backyard_size"] - param["q0"])
         / (param["backyard_size"]))
        - (param["beta"]
           * (income_net_of_commuting_costs[0, :]
              - (capital_destroyed * param["subsidized_structure_value"]))
           / (param["backyard_size"] * R))
    )

Back to the compute_outputs function, the housing supply per unit of available land for informal settlements is just set as 1 km²/km². Indeed, as absentee landlords do not have outside use for their land, they face no opportunity cost when renting it out, and therefore rent out all of it. We also remind the reader that the informal backyard and settlement dwellings are not capital-intensive, to the extent that they have a fixed size and cover only one floor. The housing supply is therefore equal to the land supply. Again, this is a simplification, but we believe that this is a good enough approximation of reality.

Equilibrium number of households

At the end of the compute_outputs function, we just divide the housing supply per unit of available land by the dwelling size, and multiply it by the amount of available land to obtain the number of households by housing type in each grid cell. Then, we associate people in each selected pixel to the highest bidding income group (here denoted \(i\)):

\[N_i^h(x) = \frac{s_h(x)L_h(x)}{Q_h(x,i,u)}\]

From there, we are able to recover the total number of households in each income group for a given housing type:

    # Yields population density in each selected pixel
    people_init = housing_supply / dwelling_size * (np.nansum(limit, 0) > 0)
    people_init[np.isnan(people_init)] = 0
    # Yields number of people per pixel, as 0.25 is the area of a pixel
    # (0.5*0.5 km) and coeff_land reduces it to inhabitable area
    people_init_land = people_init * coeff_land * 0.25

    # We associate people in each selected pixel to the highest bidding income
    # group
    people_center = np.array(people_init_land)[None, :] * proba
    people_center[np.isnan(people_center)] = 0
    # Then we sum across pixels and get the number of people in each income
    # group for given housing type
    job_simul = np.nansum(people_center, 1)

Also note that we ensure that the housing rent in the formal private sector is larger than the agricultural rent:

    if housing_type == 'formal':
        R = np.maximum(R, agricultural_rent)

Iteration and results

Back to the body of the compute_equilibrium function, we sum the outputs of the compute_outputs function across grid cells to get the total number of households in each income group. Then, we define an error metric error_max_abs comparing this result with values from the data, and an incremental term diff_utility (depending on a predetermined convergence factor):

    #  We first update the first iteration of output vector with the sum of
    #  simulated people per income group across housing types (no RDP)
    total_simulated_jobs[index_iteration, :] = np.sum(
        simulated_jobs[index_iteration, :, :], 0)

    #  diff_utility will be used to adjust the utility levels
    #  Note that optimization is made to stick to households_per_income_class,
    #  which does not include people living in RDP (as we take this as
    #  exogenous)

    #  We compare total population for each income group obtained from
    #  equilibrium condition (total_simulated_jobs) with target population
    #  allocation (households_per_income_class)

    #  We arbitrarily set a strictly positive minimum utility level at 10
    #  (as utility will be adjusted multiplicatively, we do not want to break
    #  the model with zero terms)

    diff_utility[index_iteration, :] = np.log(
        (total_simulated_jobs[index_iteration, :] + 10)
        / (households_per_income_class + 10))
    diff_utility[index_iteration, :] = (
        diff_utility[index_iteration, :] * param["convergence_factor"])
    (diff_utility[index_iteration, diff_utility[index_iteration, :] > 0]
     ) = (diff_utility[index_iteration, diff_utility[index_iteration, :] > 0]
          * 1.1)

    # Difference with reality
    error[index_iteration, :] = (total_simulated_jobs[index_iteration, :]
                                 / households_per_income_class - 1) * 100
    #  This is the parameter of interest for optimization
    error_max_abs[index_iteration] = np.nanmax(
        np.abs(total_simulated_jobs[index_iteration, :]
               / households_per_income_class - 1))

As long as the error metric is above a predetermined precision level (precision), and the number of iterations is below a predetermined threshold (max_iter), we repeat the process described above after updating the utility levels with the incremental term:

            # When population is overestimated, we augment utility to reduce
            # population (cf. population constraint from standard model)
            utility[index_iteration, :] = np.exp(
                np.log(utility[index_iteration - 1, :])
                + diff_utility[index_iteration - 1, :])

Note that we also update the convergence factor to help the algorithm converge.

            # NB: we assume the minimum error is 100 not to break model with
            # zeros
            convergence_factor = (
                param["convergence_factor"] / (
                    1
                    + 0.5 * np.abs(
                        (total_simulated_jobs[index_iteration, :] + 100)
                        / (households_per_income_class + 100)
                        - 1)
                    )
                )

            # We also reduce it as time passes, as errors should become smaller
            # and smaller
            convergence_factor = (
                convergence_factor
                * (1 - 0.6 * index_iteration / param["max_iter"])
                )

To complete the process, we concatenate (exogenous) values for formal subsidized housing to our final output vectors while taking care that all values have the same units:

    #  We correct output coming from data_RDP with more reliable estimations
    #  from SAL data (to include council housing)
    households_RDP = (number_properties_RDP * total_RDP
                      / sum(number_properties_RDP))
    #  Share of housing (no backyard) in RDP surface (with land in km²)
    construction_RDP = np.matlib.repmat(
        param["RDP_size"] / (param["RDP_size"] + param["backyard_size"]),
        1, len(grid_temp.dist))
    #  RDP dwelling size (in m²)
    dwelling_size_RDP = np.matlib.repmat(
        param["RDP_size"], 1, len(grid_temp.dist))

    # NB: we multiply by construction_RDP because we want the housing supply
    # per unit of AVAILABLE land: RDP building is only a fraction of overall
    # surface (also accounts for backyarding)
    housing_supply_RDP = (
        construction_RDP * dwelling_size_RDP * households_RDP
        / (coeff_land_full[3, :] * 0.25)
        )
    housing_supply_RDP[np.isnan(housing_supply_RDP)] = 0
    dwelling_size_RDP = dwelling_size_RDP * (coeff_land_full[3, :] > 0)
    initial_state_dwelling_size = np.vstack(
        [dwelling_size_export, dwelling_size_RDP])
    # Note that RDP housing supply per unit of available land has nothing to do
    # with backyard housing supply per unit of available land
    initial_state_housing_supply = np.vstack(
        [housing_supply_export, housing_supply_RDP]
        )

We also return other outputs from the model, such as utility levels, the final error, or capital per unit of available land.

Subsequent periods

Back to the body of the main_nb script, we save the outputs for the initial state equilibrium in a dedicated subfolder (according to the naming convention defined in the preamble). Then, we launch the run_simulation function that takes them as an argument, and calls on the same modules as before, plus the functions_dynamic.py module.

After initializing a few key variables, the function starts a loop over predefined simulation years. The first part of the loop consists in updating the value of all time-moving variables. This is based on exogenous scenarios previously imported as inputs (through the import_scenarios function) and taken as an argument of the function. Provided by the CoCT, they provide trajectories for the following set of variables:

• Income distribution

• Inflation rate

• Interest rate

• Total population

• Price of fuel

• Land use

This leads to the update of, among others, number of households per income class, expected income net of commuting costs, capital values of formal subsidized and informal dwelling units:

            (average_income, households_per_income_class
             ) = eqdyn.compute_average_income(
                spline_population_income_distribution,
                spline_income_distribution, param, year_temp)
            income_net_of_commuting_costs = np.load(
                precalculated_transport + "GRID_incomeNetOfCommuting_"
                + str(int(year_temp)) + ".npy")
            (param["subsidized_structure_value"]
             ) = (param["subsidized_structure_value_ref"]
                  * (spline_inflation(year_temp) / spline_inflation(0)))
            (param["informal_structure_value"]
             ) = (param["informal_structure_value_ref"]
                  * (spline_inflation(year_temp) / spline_inflation(0)))
            mean_income = spline_income(year_temp)
            interest_rate = eqdyn.interpolate_interest_rate(
                spline_interest_rate, year_temp)
            population = spline_population(year_temp)
            total_RDP = spline_RDP(year_temp)
            minimum_housing_supply = spline_minimum_housing_supply(year_temp)
            number_properties_RDP = spline_estimate_RDP(year_temp)

Note that we also update the scale factor of the Cobb-Douglas housing production function so as to neutralize the impact that inflation of incomes would have on housing supply through rents 23:

            construction_param = (
                (mean_income / param["income_year_reference"])
                ** (- param["coeff_b"]) * param["coeff_A"]
            )

This is because we build a stable equilibrium model with rational agents. In particular, this requires to remove money illusion (i.e., the tendency of households to view their wealth and income in nominal terms, rather than in real terms).

Also note that we are updating land availability coefficents, as they evolve through time, and agricultural rent, which also depends on the interest rate and the updated scale factor:

            coeff_land = inpdt.import_coeff_land(
                spline_land_constraints, spline_land_backyard,
                spline_land_informal, spline_land_RDP, param, year_temp)
            agricultural_rent = inpprm.compute_agricultural_rent(
                spline_agricultural_price(year_temp), construction_param,
                interest_rate, param, options)

Then, we proceed in three steps. We first compute a new unconstrained equilibrium with the updated variables. We then compute the targeted difference between the final value of formal private housing supply at \(t+1\) and the one at \(t\), through the evolution_housing_supply function:

            deriv_housing_temp = eqdyn.evolution_housing_supply(
                housing_limit, param, years_simulations[index_iter],
                years_simulations[index_iter - 1], tmpi_housing_supply[0, :],
                stat_temp_housing_supply[0, :])

This law of motion reflects the fact that formal private housing stock depreciates with time and that developers respond to price incentives with delay as in Viguie and Hallegatte [2012], hence might differ from the one computed as an unconstrained equilibrium output. Formally, this corresponds to:

\[s_{FP}(x|t+1) - s_{FP}(x|t)\]

\[\begin{split}= \begin{cases} \frac{s_{FP}^{eq}(x|t+1) - s_{FP}(x|t)}{\tau} - (\rho + \textcolor{green}{\rho_{FP}^{struct}(x)}) s_{FP}(x|t) & \text{if $s_{FP}(x|t) < s_{FP}^{eq}(x|t+1)$} \\ -(\rho + \textcolor{green}{\rho_{FP}^{struct}(x)}) s_{FP}(x|t) & \text{if $s_{FP}(x|t) \geq s_{FP}^{eq}(x|t+1)$} \end{cases}\end{split}\]

In the body of the evolution_housing_supply function, this translates into:

        diff_housing = ((housing_supply_1 - housing_supply_0)
                        * (housing_supply_1 > housing_supply_0)
                        * (t1 - t0) / param["time_invest_housing"]
                        - housing_supply_0 * (t1 - t0)
                        * param["depreciation_rate"])

Finally, we compute a new equilibrium under this constraint, which yields our final outputs at \(t+1\). Concretely, we set the value of housing supply at \(t+1\) as being the sum of the housing supply at \(t\) plus the difference we just computed, and store it under the housing_in parameter (whose default value does not matter). In the body of the run_simulations function, this looks like:

            param["housing_in"] = stat_temp_housing_supply[0, :]
            + deriv_housing_temp

Then, we run the compute_equilibrium function with the modified option that developers do not adjust their housing supply anymore (so that housing_supply = housing_in in the body of the compute_housing_supply_formal function). All outputs will then be re-computed to fit this fixed target housing supply.

Back to the body of the main_nb script, we save the simulation outputs in a dedicated subfolder, that will be used for output visualization.

Outputs

Apart from the data visualization in notebooks, all the modules of this package are used as part of the plots scripts. The plots_inputs.py script plots input data for descriptive statistics. The plots_equil.py script plots outputs specific to the initial state equilibrium, notably with respect to result validation. The plots_simul.py script plots outputs for all simulation years, and some evolution of variables across time. Only the two latter require to run the main_nb script at least once to save the associated numeric outputs. To call on a specific simulation, one just has to change the path name at the beginning of the scripts to call on the dedicated subfolder. All scripts save the associated tables and figures in another subfolder (under the same name for equilibrium and simulation outputs).

Then, plots_use_case_anticip.py and plots_use_case_cchange.py draw on outputs from plots_equil.py to generate plots and tables for specific comparative statics (with and without options["agents_anticipate_floods"] in the first case, with and without options["climate_change"] in the second case). Those outputs are the ones leveraged in the Notebook: use cases section (also see corresponding notebooks).

As part of the outputs package, the export_outputs.py module is for processing and exporting the standard urban variables of the model (already present in Pfeiffer et al. [2019]), the flood_outputs.py module is for processing values relative to floods, and the export_outputs_floods.py module is for exporting them. We believe the code here to be self-explanatory enough, and refer the reader to API reference for further details.

Calibration

This package is essentially called as part of the calib_nb notebook. Note that it is only useful to run this script if the underlying data used for calibration has changed, as all necessary parameters have been pre-calibrated. Also note that it takes time to run. Most of the calibration process relies on the estimation of partial relations derived from the general equilibrium model 24. It is therefore essential to have a good understanding of the Equilibrium section to understand this part.

The preamble of the calib_nb notebook starts with the same imports as the main_nb notebook, then does some more data preparation. Essentially, it defines an observed dominant income group and number of formal private units (useful variables for what follows), and a sample selection array for areas where formal private housing units is predominant. This processing is done at the Small Place (SP) level, and ensures that the relations we are going to estimate are well identified: indeed, many of them rely on equilibrium conditions that are only defined for the formal private sector. Note that, whereas the same data might be used for calibration of parameters and validation of results, it is never an input of the model per se: we want to validate / calibrate the model with external data, for the fit not to be automatic.

The rest of the script calls on the calib_main_func.py module, that itself calls on other modules from the sub directory.

Housing production function parameters

We start by calibrating housing production function parameters using the estim_construct_func_param function. From the equilibrium formulas for housing supply and number of households, we have the following relation:

\[\frac{N^{FP}(x)Q_{FP}(x)}{L_{FP}(x)} = \kappa^{\frac{1}{a}} (\frac{(1-a)R_{FP}(x)}{\rho + \textcolor{green}{\rho_{FP}^{struct}(x)} + \delta})^{\frac{1-a}{a}}\]

Log-linearizing it (and using the relation between price and rent that we already used to define agricultural rent) allows us to identify the following linear regression, which we estimate with data at the SP level \(s\) (instead of the grid-cell level \(x\), due to data availability constraints):

\[log(N_s^{FP}) = \gamma_1 + \gamma_2 log(P_s) + \gamma_3 log(Q_s) + \gamma_4 log(L_s^{FP}) + \epsilon_s\]

• \(\gamma_1 = log(\kappa (\frac{1-a}{a})^{1-a})\)

• \(\gamma_2 = 1-a\)

• \(\gamma_3 = -1\)

• \(\gamma_4 = 1\)

We therefore have \(a = 1 - \gamma_2\) and \(\kappa = (\frac{a}{1-a})^{1-a} exp(\gamma_1)\).

In the code, this translates into:

    # We define our outcome variable
    y = np.log(data_number_formal[selected_density])
    # We define our independent variables
    # Note that we use data_sp["unconstrained_area"] (which is accurate data at
    # SP level) rather than coeff_land (which is an estimate at grid level)
    X = np.transpose(
        np.array([np.ones(len(data_sp["price"][selected_density])),
                  np.log(data_sp["price"][selected_density]),
                  np.log(data_sp["dwelling_size"][selected_density]),
                  np.log(param["max_land_use"]
                         * data_sp["unconstrained_area"][selected_density])])
        )
    # NB: Our data set for dwelling sizes only provides the average dwelling
    # size at the Sub-Place level, aggregating formal and informal housing

    # We run the linear regression
    modelSpecification = sm.OLS(y, X, missing='drop')
    model_construction = modelSpecification.fit()
    print(model_construction.summary())
    parametersConstruction = model_construction.params

    # We export outputs of the model
    coeff_b = parametersConstruction["x1"]
    coeff_a = 1 - coeff_b
    # Scale factor formula comes from zero profit condition combined with
    # footnote 16 from Pfeiffer et al. (typo in original paper)
    if options["correct_kappa"] == 1:
        coeffKappa = ((1 / (coeff_b / coeff_a) ** coeff_b)
                      * np.exp(parametersConstruction["const"]))
    elif options["correct_kappa"] == 0:
        coeffKappa = ((1 / (coeff_b) ** coeff_b)
                      * np.exp(parametersConstruction["const"]))

Note that we run our regression on the restricted sample defined by the selected_density variable.

Incomes and gravity parameter

We update the parameter vector with the newly calculated values and go on with the calibration of incomes \(y_{ic}\) and the gravity parameter \(\lambda\) (see Commuting choice model for more details and definitions).

In practice, we scan a set of predefined values for the parameter \(\lambda\) over which we determine the value of \(y_{ic}\). We then aggregate the total distribution of residence-workplace distances, and compare it with the data aggregated from Cape Town’s Transport Survey 2013. We select the value of \(\lambda\), and the associated \(y_{ic}\), that minimize a distance score between the computed distribution of commuting distances and aggregates from the data.

In the code, this is done through the estim_incomes_and_gravity function. First, it imports the number of workers per income group in each selected job center (defined at the Transport Zone level) through the import_employment_data function (from the module of the same name).

Transport costs

Then, it imports transport costs through the import_transport_costs function (from the compute_income.py module).

The first part of this function imports data on transportation times and distances (at the SP level), and estimates of public transportation fixed (over one month) and variable costs, based upon linear regressions using data from Roux [2013] (table 4.15). It also imports fuel prices for the variable component of private transportation costs, and 400 rands as the monthly depreciation cost of a vehicle for their fixed component.

In a second part, the function computes the total yearly monetary cost of commuting for one household over round trips:

    # Note that we do have some negative durations: their number is small,
    # so we just convert them to zero
    timeOutput[:, :, 0] = (transport_times["distanceCar"]
                           / param["walking_speed"] * 60 * 60 * 1.2 * 2)
    timeOutput[:, :, 0][np.isnan(transport_times["durationCar"])] = 0
    timeOutput[:, :, 1] = copy.deepcopy(transport_times["durationTrain"])
    timeOutput[:, :, 1][transport_times["durationTrain"] < 0] = 0
    timeOutput[:, :, 2] = copy.deepcopy(transport_times["durationCar"])
    timeOutput[:, :, 2][transport_times["durationCar"] < 0] = 0
    timeOutput[:, :, 3] = copy.deepcopy(transport_times["durationMinibus"])
    timeOutput[:, :, 3][transport_times["durationMinibus"] < 0] = 0
    timeOutput[:, :, 4] = copy.deepcopy(transport_times["durationBus"])
    timeOutput[:, :, 4][transport_times["durationBus"] < 0] = 0

    # Length (in km) using each mode
    if options["correct_round_trip"] == 1:
        multiplierPrice = np.empty((timeOutput.shape))
        multiplierPrice[:] = np.nan
        multiplierPrice[:, :, 0] = np.zeros((timeOutput[:, :, 0].shape))
        multiplierPrice[:, :, 1] = transport_times["distanceCar"] * 2
        multiplierPrice[:, :, 2] = transport_times["distanceCar"] * 2
        multiplierPrice[:, :, 3] = transport_times["distanceCar"] * 2
        multiplierPrice[:, :, 4] = transport_times["distanceCar"] * 2
    elif options["correct_round_trip"] == 0:
        multiplierPrice = np.empty((timeOutput.shape))
        multiplierPrice[:] = np.nan
        multiplierPrice[:, :, 0] = np.zeros((timeOutput[:, :, 0].shape))
        multiplierPrice[:, :, 1] = transport_times["distanceCar"]
        multiplierPrice[:, :, 2] = transport_times["distanceCar"]
        multiplierPrice[:, :, 3] = transport_times["distanceCar"]
        multiplierPrice[:, :, 4] = transport_times["distanceCar"]

    # Convert the results to annual cost
    pricePerKM = np.empty(5)
    pricePerKM[:] = np.nan
    pricePerKM[0] = np.zeros(1)
    pricePerKM[1] = priceTrainPerKM*numberDaysPerYear
    pricePerKM[2] = priceFuelPerKM*numberDaysPerYear
    pricePerKM[3] = priceTaxiPerKM*numberDaysPerYear
    pricePerKM[4] = priceBusPerKM*numberDaysPerYear

    # Monetary price per year (for each employment center)
    # NB: 12 is for number of months in a year
    monetaryCost = np.zeros((185, timeOutput.shape[1], 5))
    for index2 in range(0, 5):
        monetaryCost[:, :, index2] = (pricePerKM[index2]
                                      * multiplierPrice[:, :, index2])
    #  Train
    monetaryCost[:, :, 1] = monetaryCost[:, :, 1] + priceTrainFixedMonth * 12
    #  Private car
    monetaryCost[:, :, 2] = (monetaryCost[:, :, 2] + priceFixedVehiculeMonth
                             * 12)
    #  Minibus/taxi
    monetaryCost[:, :, 3] = monetaryCost[:, :, 3] + priceTaxiFixedMonth * 12
    #  Bus
    monetaryCost[:, :, 4] = monetaryCost[:, :, 4] + priceBusFixedMonth * 12

In a third and last part, it computes the time opportunity cost parameter (i.e., the fraction of working time spent commuting):

    # Daily share of working time spent commuting (all values in sec)
    # NB: The time cost parameter is a proportionality factor between time
    # and monetary values. By default, it is set as 1: the welfare loss from
    # time spent commuting directly translates into foregone wages.
    costTime = (timeOutput * param["time_cost"]
                / (60 * 60 * numberHourWorkedPerDay))

Income calculation

The estim_incomes_and_gravity function then goes on with the calibration of incomes per se. To do so, it calls on the EstimateIncome function (also from the compute_income.py module):

Essentially, this function relies on the following equation (that can be recovered following Commuting choice model):

\[W_{ic} = \chi_i \sum_{s} \pi_{c|is} N_{is}\]

• \(W_{ic}\) is the number of households of income group \(i\) who work in job center \(c\).

• \(\chi_i\) is the employment rate of households in income group \(i\) (household_size parameter divided by 2).

• \(\pi_{c|is}\) is the probability to choose to work in location \(c\) given residential location \(s\) (SP level) and income group \(i\).

• \(N_{is}\) is the number of households of income group \(i\) living in residential location \(s\).

All the terms in the above equation are observed, except for incomes \(y_{ic}\) (implicit in the definition of \(\pi_{c|is}\)). For each scanned value of \(\lambda\) and each income group, the value of incomes will therefore be updated in accordance to some error term until it falls below a given precision level:

            # Then we iterate by adding to each job center income the average
            # value of income per income group, weighted by the importance of
            # the error relative to the observed job center population: if we
            # underestimate the population, we increase the income
            while ((iter <= maxIter - 1) & (errorMax > tolerance)):

                incomeCenters[:, iter] = (
                    incomeCenters[:, max(iter-1, 0)]
                    + factorConvergenge
                    * averageIncomeGroup
                    * error[:, max(iter - 1, 0)]
                    / popCenters
                )

                # We also update the error term and store some values
                # before iterating over
                error[:, iter], _ = commutingSolve(
                    incomeCenters[:, iter], averageIncomeGroup, popCenters,
                    popResidence, monetary_cost, costTime, param_lambda,
                    householdSize, whichCenters, bracketsDistance,
                    distanceOutput, options)

                errorMax = np.nanmax(
                    np.abs(error[:, iter] / popCenters))
                scoreIter[iter] = np.nanmean(
                    np.abs(error[:, iter] / popCenters))

                iter = iter + 1

Note that the convergence factors are numerical parameters with no interpretation per se, that are fine-tuned by trial and error to help convergence.

Both the error term and the simulated distribution of residence-workplace distances are obtained as outputs of the commutingSolve function. Let us dig into its body. First, it computes the probability \(\pi_{c|is}\) by calling on the compute_ODflows function (again, see Commuting choice model for more details on this function). Then, it simply defines the error term as the difference between the two sides of the above equation:

    # NB: correction is not needed a priori, as income distribution data from
    # SP does not include people out of employment
    if options["correct_eq3"] == 1:
        score = (popCenters
                 - (householdSize / 2
                    * np.nansum(popResidence[None, :] * ODflows, 1))
                 )
    elif options["correct_eq3"] == 0:
        score = (popCenters
                 - np.nansum(popResidence[None, :] * ODflows, 1))

Finally, it defines the number of commuters per distance bracket in aggregate data (same as residence-workplace distance distribution) by collapsing the right-hand side of the equation into those brackets:

    nbCommuters = np.zeros(len(bracketsDistance) - 1)
    for k in range(0, len(bracketsDistance)-1):
        which = ((distanceOutput[whichCenters, :] > bracketsDistance[k])
                 & (distanceOutput[whichCenters, :] <= bracketsDistance[k + 1])
                 & (~np.isnan(distanceOutput[whichCenters, :])))
        if options["correct_eq3"] == 1:
            nbCommuters[k] = (
                np.nansum(which * ODflows * popResidence[None, :])
                * (householdSize / 2)
                )
        elif options["correct_eq3"] == 0:
            nbCommuters[k] = (
                np.nansum(which * ODflows * popResidence[None, :]))

Parameter selection

Back to the body of the estim_incomes_and_gravity function, we import the residence-workplace distance distribution observed in the data, and define Bhattacharyya distance as our score. Then, we simply select the gravity-income pair that minimizes this metric:

    # Residence-workplace distance distribution comes from the CoCT's 2013
    # Transport Survey
    data_distance_distribution = np.array(
        [45.6174222, 18.9010734, 14.9972971, 9.6725616, 5.9425438, 2.5368754,
         0.9267125, 0.3591011, 1.0464129])

    # Compute accessibility index
    # NB1: Bhattacharyya distance measures the similarity of two probability
    # distributions (here, data vs. simulated % of commuters)
    # NB2: Mahalanobis distance is a particular case of the Bhattacharyya
    # distance when the standard deviations of the two classes are the same
    bhattacharyyaDistances = (
        - np.log(np.nansum(np.sqrt(data_distance_distribution[:, None]
                                   / 100 * distanceDistribution), 0))
        )
    whichLambda = np.argmin(bhattacharyyaDistances)

    # Hence, we keep the lambda that minimizes the distance and the associated
    # income vector
    lambdaKeep = list_lambda[whichLambda]
    incomeCentersKeep = incomeCenters[:, :, whichLambda]

Note that we rely on this two-step computation-selection procedure as a simplification for a more complex nested optimization (as the value of the distance score itself depends on the value of calibrated incomes): given the fine discrete range that we use for scanning (see scan_type option), we consider our results as a good enough approximation of true parameter values (as long as we stay at the interior of the scanned range).

Utility function parameters

We update the parameter vector with the newly calculated values and go on with the calibration of utility function parameters through the estim_util_func_param function. It allows to optimize over the parameters \(\beta\), \(q_0\), and the utility levels of various income groups (hence, indirectly, the local amenity index \(A(x)\)) 25. To do so, it fits three data moments where those variables enter, as they cannot be identified separately from the model structure otherwise. More precisely, it is going to maximize a composite log-likelihood that sums one log-likelihood for the fit of the predicted local amenity index on exogenous amenities, one for the fit of predicted income sorting, and one for the fit of predicted dwelling sizes 26.

We are going to describe this process in more details, as it is the one followed in Pfeiffer et al. [2019], but before that, we are going to explain why we actually only use the first data moment in our benchmark specification.

External calibration

First of all, note that the procedure we just described is a complex optimization problem that requires us to run a prior discrete parameter scanning before running a smooth optimization algorithm (such as gradient descent, etc.), to ensure that we start in the interior set of feasible solutions (which is not obvious a priori given the multi-dimensionality of the problem). Then, even within this set, we may not face unique solutions. We therefore suggest a way to reduce the dimensionality of the problem, at the same time as improving the empirical validity of our estimates.

For a start, the parameter \(q_0\) has a direct empirical interpretation: it can just be set to be equal to the bottom decile, or bottom percentile, of observed dwelling sizes. Since we do not have access to such data (but only to average dwelling sizes aggregated at the SP level), we just keep the value calibrated in Pfeiffer et al. [2019], which is plausible enough, to be substituted later with a more robust value: although this approach may seem more rudimentary than the full one, it requires no structural assumptions whatsoever.

It is different for the \(\beta\) parameter. Its empirical counterpart would be the expenditure share of households on housing (at purchasing power parity). However, direct measurement of such quantity in expenditure survey data suffers from numerous biases, as we do not observe annual spending by owner-occupiers (as opposed to renters), and we do not observe variation in local housing prices either (see Diamond and Gaubert [2022] for more details). Then, due to non-homotheticity (households spend a smaller share of their budget on housing as their income increases), this share is expected to vary across income groups. Yet, it is the whole point of using a Stone-Geary (as opposed to Cobb-Douglas) specification to micro-found such non-homotheticity with a single elasticity parameter 27.

For all those reasons, we need to leverage some theoretical structure to estimate this parameter. However, whereas the Cobb-Douglas specification used for the housing production function has been shown to be empirically robust [Combes et al., 2021], it is not the case for Stone-Geary preferences, which should rather be thought of as a first-order approximation for non-homothetic constant elasticity of substitution (NHCES) preferences or price independent generalized linear (PIGL) preferences 28 [Finlay and Williams, 2022]. Therefore, we think it is more generally valid to directly use the benchmark estimate for the \(\beta\) parameter (which also controls for the aforementioned biases) from this last paper, instead of trying to estimate it ourselves (with endogenous moments). Luckily for us, it is almost the same as the value estimated by Pfeiffer et al. [2019]. We therefore keep that value in the code, and do not contradict previous findings (even though we discuss the corresponding method).

Then, we are simply left with the estimation of the local amenity score \(A(x)\), that we are going to detail below. A last general comment we want to make is that, even for a well-identified model, it is important to run sensitivity checks on the value of parameters: for internal calibration, this implies checking alternative data processing and sample selection ; for external calibration, this implies scanning through acceptable ranges of values (more on that in the code). Running the calibration with data from previous years is also a good robustness check to determine how close our estimates are to the long-term equilibrium values we are targeting.

Fit on exogenous amenities

Back to the body of the estim_util_func_param function, we define a less stringent selection array than selected_density to maintain predictive power (with a high enough number of observations) while potentially losing some empirical validity (remember that our theoretical relations are only valid for the formal private sector):

    selectedSP = (
        (data_number_formal > 0.90 * housing_types_sp.total_dwellings_SP_2011)
        & (data_income_group > 0)
        )

After pinning down the values of \(\beta\) and \(q_0\), we define target utility levels close to what is expected as an equilibrium outcome:

    utilityTarget = np.array([1200, 4800, 16000, 77000])

Since, in practice, the poorest income group is going to be crowded out of the formal private sector, we are only going to optimize over the utility levels of the three richest income groups. For the sake of numerical simplicity, we are even going to take the lowest utility level as fixed, and allow only the two highest to vary (note that none of this is critical for convergence):

    listVariation = np.arange(0.5, 1.5, 0.01)
    initUti2 = utilityTarget[1]
    listUti3 = utilityTarget[2] * listVariation
    listUti4 = utilityTarget[3] * listVariation

Indeed, based on households’ first-order optimality conditions, the predicted value of the amenity score is going to depend on all of the above through the formula:

\[A_s = \frac{u_{i(s)}}{(1 - \beta)^{1 - \beta} \beta ^{\beta}} \frac{\tilde{y}_s - q_0 R_s}{R_s ^{\beta}}\]

• \(u_{i(s)}\) is the utility level of the dominant income group \(i\) in Small Place \(s\).

• \(\tilde{y}_s\) is the expected income net of commuting costs of the dominant income group in Small Place \(s\).

• \(R_s\) is the observed annual rent (per m²) in Small Place \(s\).

Note that, since we only observe housing prices in transaction data, we define \(R_s\) as the flow value of the underlying housing asset:

    dataRent = data_sp["price"] * interest_rate

Also note that we are not interested in the value of the utility levels per se at this stage, but only in the value of the amenity score. We could therefore directly optimize over that value. The reason why we keep the above specification is that it becomes important when we also want to optimize over \(\beta\) and \(q_0\). Then, if we are only interested in the calibration of the amenity score, we believe it is more robust to estimate only the fit with regard to exogenous amenities. Indeed, this implies very light structural assumptions compared to other moments, and it ensures that the amenity score is well-identified. The score has an impact on the other two moments, but if we allow them to enter the calibration, then it would also capture part of the residual fit of the model (i.e., the part not explained by amenity factors). Therefore, sticking with the first data moment allows the amenity score to have a clear empirical interpretation, which can also be leveraged for policy evaluation (studying how a change in exogenous coviarates eventually impacts spatial sorting). Still, using more moments becomes important to avoid underidentification when we want to estimate more interacting parameters, even if it comes at the price of tractability.

Then, we just import amenity data with the import_exog_amenities function and select exogenous covariates before calling on the EstimateParametersByScanning function that runs the discrete parameter scan. This function runs some additional sample and variable selection, then defines useful functions for the optimization algorithm, before running the algorithm per se:

    # %% FUNCTIONS USED FOR THE FIT ON DWELLING SIZE AND AMENITIES

    # Relationship between rents and dwelling sizes (see technical
    # documentation)
    CalculateDwellingSize = (
        lambda beta, basic_q, incomeTemp, rentTemp:
            beta * incomeTemp / rentTemp + (1 - beta) * basic_q
            )

    # Log likelihood for a lognormal law of mean 0: we will assume that
    # dwelling size and amenity residuals follow such a law (see math
    # appendix)
    ComputeLogLikelihood = (
        lambda sigma, error:
            np.nansum(- np.log(2 * math.pi * sigma ** 2) / 2
                      - 1 / (2 * sigma ** 2) * (error) ** 2)
            )

    # %% OPTIMIZATION ALGORITHM

    # We decide whether we want to use GLM or OLS estimation for the fit on
    # exogenous amenities.
    # Note that GLM is not stable in this version of the code (default option
    # set as zero)
    optionRegression = options["glm"]

    # Initial value of parameters (all possible combinations)
    # Note that we do not consider spatial autocorrelation
    combinationInputs = np.array(
        np.meshgrid(listBeta, listBasicQ, listUti3, listUti4)).T.reshape(-1, 4)

    # Initial score (log-likelihood) values for each regression
    # Note that fit on housing supply / building density is included, as the
    # estimation (where it will be cancelled out) is done in the
    # calibration.sub.loglikelihood module.
    scoreAmenities = - 10000 * np.ones(combinationInputs.shape[0])
    scoreDwellingSize = - 10000 * np.ones(combinationInputs.shape[0])
    scoreIncomeSorting = - 10000 * np.ones(combinationInputs.shape[0])
    scoreHousing = - 10000 * np.ones(combinationInputs.shape[0])
    scoreTotal = - 10000 * np.ones(combinationInputs.shape[0])

    print('\nStart scanning')
    print('\n')

    # We update the scores for each set of parameters
    # Note that
    for index in range(0, combinationInputs.shape[0]):
        # print(index)
        (scoreTotal[index], scoreAmenities[index], scoreDwellingSize[index],
         scoreIncomeSorting[index], scoreHousing[index], parametersAmenities,
         modelAmenities, parametersHousing) = callog.LogLikelihoodModel(
             combinationInputs[index, :], initUti2, net_income,
             groupLivingSpMatrix, dataDwellingSize, selectedDwellingSize,
             dataRent, selectedRents, predictorsAmenitiesMatrix,
             tableRegression, variablesRegression, CalculateDwellingSize,
             ComputeLogLikelihood, optionRegression, options)

    print('\nScanning complete')
    print('\n')

    # We just pick the parameters associated to the maximum score
    # Note that scoreHousing is set as zero and does not impact parameter
    # selection.

    # By default, we cancel out the scores associated with observed dwelling
    # sizes and income sorting: this is because the fit on exogenous amenities
    # is the only relevant dimension when beta and q0 are pinned down and the
    # amenity score is the only parameter left to calibrate
    scoreDwellingSize = 0
    scoreIncomeSorting = 0

    scoreVect = (scoreAmenities + scoreDwellingSize + scoreIncomeSorting
                 + scoreHousing)
    scoreTot = np.amax(scoreVect)
    which = np.argmax(scoreVect)
    parameters = combinationInputs[which, :]

The CalculateDwellingSize function will be used as part of the third moment estimation, while the ComputeLogLikelihood function will be used for both the first and the third moment estimations. The LogLikelihoodModel function (defined as part of the loglikelihood module) returns the values of the log-likelihoods associated with each data moment. Note how we set the log-likelihoods associated with the fit on dwelling sizes and income sorting to zero before maximizing the composite log-likelihood (scoreHousing is also set to zero as part of the LogLikelihoodModel function, and serves as a placeholder for an additional data moment used in alternative versions of NEDUM-2D): this is where we decide to focus only on the first data moment.

As part of the LogLikelihoodModel function, we finally define the log-likelihood associated with the fit on exogenous amenities. Consider the following relation:

\[A_s = (\prod_{n} (a_{n,s})^{\mathcal{v}_i}) \epsilon_{A,s}\]

• \(a_{n,s}\) are exogenous amenity covariates at the SP level.

• \(\mathcal{v}_i\) are elasticity parameters to be estimated (conditional on the dominant income group at the SP level).

• \(\epsilon_{A,s}\) is an error term that is log-normally distributed with mean zero.

Log-linearizing this relation, we can regress the predicted value of the log-amenity score on log-values of exogenous amenities that we proxy as dummy variables (pre-processing is already done as part of the import_exog_amenities function), and estimate the parameters \(\mathcal{v}_i\) by ordinary least squares (OLS). In the code, this yields:

    # Theoretical formula for log amenity index (from technical documentation)
    # Note that we stay under sample selection from selectedRents variable
    logAmenityIndex = (
        np.log(np.array(Uo)[:, None])
        - np.log(
            (1 - beta) ** (1 - beta) * beta ** beta
            * (net_income[:, selectedRents]
               - basicQ * np.array(dataRent)[None, selectedRents])
            / (np.array(dataRent)[None, selectedRents] ** beta))
        )
    # We select values for dominant income groups only and flatten the array:
    # this allows to select the appropriate net income and utility to identify
    # the regression
    logAmenityIndex = np.nansum(
        logAmenityIndex * groupLivingSpMatrix[:, selectedRents], 0)
    # logAmenityIndex[np.abs(logAmenityIndex.imag) > 0] = np.nan
    # logAmenityIndex[logAmenityIndex == -np.inf] = np.nan

    # We get residuals for the regression of log amenity index on exogenous
    # dummy variables.
    # Note that we identify dummies with logs of original amenity values
    # (normalized to take values between 1 and e): see technical documentation

    # OLS estimation
    if (optionRegression == 0):
        A = predictorsAmenitiesMatrix  # [~np.isnan(logAmenityIndex), :]
        y = (logAmenityIndex[~np.isnan(logAmenityIndex)]).real
        # parametersAmenities, residuals, rank, s = np.linalg.lstsq(A, y,
        #                                                           rcond=None)
        # res = scipy.optimize.lsq_linear(A, y)
        # parametersAmenities = res.x
        # residuals = res.fun
        modelSpecification = sm.OLS(y, A, missing='drop')
        modelAmenities = modelSpecification.fit()
        parametersAmenities = modelAmenities.params
        errorAmenities = modelAmenities.resid_pearson

This also allows us to recover the value of the \(\log(\epsilon_{A,s})\) residuals. Since they are normally distributed, the associated log-likelihood is directly given by the ComputeLogLikelihood function 29. Formally, this corresponds to:

\[\mathcal{L} = - \sum_n [\frac{\log(2 \pi \sigma ^2)}{2} + \frac{\epsilon ^2}{2 \sigma ^2}]\]

The calibration of the amenity score will then be completed in two steps. First, we will select the appropriate statistical model by selecting the maximum log-likelihood. Then, we will define the amenity score as the explained part of the model (i.e., the value predicted by the regressors) by taking residuals out. Back to the body of the estim_util_func_param function, this corresponds to:

    amenities_grid = calam.import_exog_amenities(
        path_data, path_precalc_inp, 'grid')
    predictors_grid = amenities_grid.loc[:, variables_regression]
    predictors_grid = sm.add_constant(predictors_grid)

        cal_amenities = np.exp(
            np.nansum(predictors_grid * parametersAmenitiesScan, 1))

Fit on income sorting

Now, suppose we also want to optimize over the \(\beta\) and \(q_0\) parameters. We will need to comment out the part of the code where we set the scores associated with the two remaining data moments to zero. Let us comment on those data moments.

Observed income sorting can be rationalized through a discrete-choice Logit model (similar to the approach we follow in Commuting choice model). According to bid-rent theory, we consider that households bid their true valuation and that land is allocated to the highest bidder. Identifying the group with the highest bids as the dominant group in the data, we can write the log-likelihood for income sorting as:

\[\mathcal{l} = \sum_s (\frac{\Psi_{i(s)}(s)}{\lambda_{inc}}) - \sum_s \log(\sum_j e^{\frac{\Psi_{j}(s)}{\lambda_{inc}}})\]

We remind the reader that \(\Psi_{j}(s)\) stands for the bid rent of some income group \(j\) in Small Place \(s\). \(\lambda_{inc}\) is a scale factor associated with the underlying Gumbel distribution of idiosyncratic tastes. It is going to increase the log-likelihood when it goes up. Note however that this impact is marginal above 10. To be conservative, while keeping the same order of magnitude as for gravity parameter \(\lambda\), we pin down this value in the code. We do not go below as it would signficantly reduce the value of the log-likelihood, and we want all the likelihoods to be of the same order so as not to overweight some data moments compared to others.

In the LogLikelihoodModel function, we simply recover the values of bid rents \(\Psi_{j}(s)\) by inverting the theoretical formula for the amenity score, with the slight modification that we allow the utility level to adapt to the income group considered (and do not fix it to the level of the dominant income group): that way, the predicted rent \(R_s\) will now reflect a distinct (unobserved) bid rent for each income group \(j\). Then, we define the log-likelihood as stated above.

Fit on dwelling sizes

Likewise, we can get a theoretical prediction for dwelling sizes based on the following relation (from households’ first-order optimality conditions):

\[q_s = \beta \frac{\tilde{y}_s}{R_s} + (1 - \beta) q_0 R_s\]

This is exactly the formula given by the CalculateDwellingSize lambda function. In the body of the LogLikelihoodModel function, we choose to define \(R_s\) as the bid rent from the observed dominant income group to capture the indirect impact of utility levels (thereby overidentifying the amenity score), but we could directly take the observed rent level as an alternative specification. Then, assuming that the true dwelling size is linked to the predicted dwelling size through a log-normally distributed error term of mean zero (\(q_s = \hat{q}_s \epsilon_{q,s}\)), we obtain the associated log-likelihood with the help of the ComputeLogLikelihood function, as we did for the fit on exogenous amenities.

Smooth optimization

After running a discrete parameter scanning in the estim_util_func_param function, the param_optim option allows the user to run a smooth optimization procedure based on the same composite log-likelihood, starting with the estimates we just computed as an initial guess. This is done by calling on the EstimateParametersByOptimization function. Note that, when pinning down the values of \(\beta\) and \(q_0\), the algorithm does not converge when setting the scores associated to dwelling sizes and income sorting to zero (directly into the LogLikelihoodModel function). For that reason, we set the default value of the param_optim option at zero and run a discrete scanning that we consider to be granular enough to estimate a precise amenity index. We therefore only recommend to use that option when allowing the \(\beta\) and \(q_0\) parameters to vary.

Disamenity index

The last part of the calibration procedure is done directly in the body of the calib_nb notebook. As we stated before, the local disamenity index associated with informal backyards and informal settlements is going to be recovered from model inversion, to proxy for unobserved disamenity factors. In other words, we are going to optimize over the value of this parameter to capture most of the residual (unexplained) component of spatial sorting into those places. This clearly improves the fit of the model, but comes at the price of empirical tractability and increases the risk of overfitting: this is the reason why we do not follow this method for other parameters when an alternative approach is available. To back up this choice, let us just say that this is not a critical factor in our simulations, and that this is also common in the literature.

We start by considering a constant value for each of the indices (one per informal housing type). This is also the approach taken by Pfeiffer et al. [2019]. We range over a discrete set of values for those parameters and select the pair that minimizes the sum of differences between total number of households in the data vs. simulation, for each housing sector of interest.

Then, we propose a procedure to improve the model fit further by allowing those parameters to vary with residential location. By default, we choose to run the procedure with the location_based_calib option set to one, but as we face a standard bias-variance trade-off when considering model fit, we allow the user to switch it off. To run it, we just disaggregate the error metric described above at the grid-cell level and start with the calibrated constant values as initial guesses for all locations. Then, we update them iteratively in proportion with the error term. We allow for a number of iterations that is large enough to reach a minimum score before the end of the algorithm.

Of course, even if we define values for all locations on the map, this parameter will only impact the model in zones where land is available for housing (same goes for the amenity index or expected income net of commuting costs).

Footnotes

1

The type of a parameter indicates whether it is plugged as a raw value or is the outcome of a calibration process. In theory, all “user” defined parameters can be overwritten by the end user. In practice, we cannot guarantee that the model runs seamlessly for all possible changes in values. We therefore encourage the end user to ask for guidance if they would like to change a parameter that was not included in main simulation runs.

2

See definition of developers’ profit function in Functional assumptions. To obtain the formula, we plug the first-order optimality condition relative to capital into the zero profit equation. Also note that we artificially set the depreciation due to floods at zero in agricultural land / at the city edge.

3

We are aware of the existence of formal (concrete) backyard structures but disregard their existence for the sake of model tractability and as they only represent a minority of all backyard settlements. Likewise, we know that some backyarding does occur within formal private backyards, but we choose to abstract from that margin. Also, we rationalize the exogeneity of informal settlement locations through the observation that most of them correspond to squatting on public land: they can therefore be seen as a (plausibly exogenous) land-use regulation choice (see Henderson et al. [2021] for an alternative model with endogenous land use).

4

Note that there is no consensus on how to enumerate RDP/BNG dwelling units, as they are counted as formal dwelling units in census data. We draw on several data sources to estimate this number (including council housing), and then allocate the units across the grid using the CoCT’s cadastre.

5

Not all the “raw” data sets (as opposed to “user” data sets that result from a calibration process and can be updated by the end user) used are actually raw data. Some of them have been pre-processed, and this explains why there are more files (used as intermediary inputs) in the projet repository than described in Key data sets. Some other files may be related to older versions of the model, or may have been imported jointly with other data sets. They are kept as reference and may serve for later implementations.

6

To some extent, this precludes mixed land use, which we do not see as a major issue given that the granularity of our setting allows us to approximate it finely.

7

More details about flood data can be found here and here. Typically, underlying prediction models consider past and forecasted precipitation and storms, current river levels, as well as soil and terrain conditions.

8

We are aware that there are other factors than maximum flood depth (such as duration and intensity) that may affect flood severity. However, partly due to data limitations, we believe that focusing on flood depth is a good first approximation.

9

More comments on the integration method used can be found here.

10

Note that we add an option to discount the most likely / less serious pluvial flood risks for formal private housing, then for formal subsidized and informal backyard structures. This is to account for the fact that such (more or less concrete) structures are better protected from run-offs, which is not an information provided by the flood maps.

11

For the purpose of this model, it is therefore equivalent to assume complete market insurance or self-insurance [Avner and Hallegatte, 2019]. We may actually have an incomplete combination of the two, which we could simulate by putting weights on our two perfect-anticipations and no-anticipations polar cases. Note however that we do not model endogenous self-protection investments, and that assessing exogenous public protection investments would require custom flood maps in the spirit of Avner et al. [2022].

12

Note that, in our framework, unemployment is taken as a phenomenon that occurs part of the year (through the household_size parameter that defines the employment rate of a household). We therefore abstract from structural unemployment phenomena. Also note that residential choice relies on the resolution of a prior commuting choice problem. Therefore, we only simulate the spatial distribution of people that are part of the labour force (with representative households accounting for two active individuals). The underlying population data (see inputs.data.import_macro_data function) covers all households living in the city (we have no information on individuals): the reweighting procedure we follow by default therefore leads us to simulate the spatial distribution of all households as if they were active, with an equal share of inactive households allocated to each income group. If we had access to more accurate data allowing us to sample out inactive households, we could follow the alternative reweighting procedure (with the unempl_reweight option) that applies a different rate to each income group based on its respective (un)employment rate, since all no-income households could then be considered as unemployed. Taking the reasoning further, we could even take people “working from home” (mostly informal labourers) out of the “active” population since they do not take part in commuting either.

13

We remind the reader that, according to the spatial indifference hypothesis, all similar households share a common (maximum attainable) utility level in equilibrium. In the model, households only differ a priori in their income class, which is why we have a unique utility level for each income class. Intuitively, the richer the household, the bigger the utility level, as a higher income translates into a bigger choice set. If such utility levels can be compared in ordinal terms, no direct welfare assessment can be derived in cardinal terms: utilities must be converted into income equivalents first. A further remark is that income levels are a proxy for household heterogeneity in the housing market. As such, they encompass several correlated dimensions (such as race). However, we have strong evidence that residential mobility is not significantly impeded by those other factors, even within the South African context, hence our focus on income as the prime determinant of spatial sorting [Dominguez-Iino and le Roux, 2022]. Also note that income groups could themselves be endogenized (including unemployment) to study interactions between the housing and the labor market, although we leave that for future work.

14

When we overestimate the population, we increase the utility level, and conversely. Indeed, a higher utility translates into a higher land consumption (all other things equal) for the same land available, hence a lower accommodable number of people.

15

In a few words, the Cobb-Douglas function used for housing production is a simple analytical form that allows to model inputs that are neither perfect substitutes or perfect complements (constant elasticity of substitution equal to one) and that enter production flexibly through calibrated total factor productivity and output elasticities. As a reminder, total factor productivity is defined as the ratio of aggregate output over aggregate inputs; and output elasticities are defined as the percentage change of output divided by the percentage change of on input. The Stone-Geary form used for households’ utility relies on the same assumptions, with the added feature that the introduction of a basic need in housing allows to model non-homothetic preferences for housing: this corresponds to a declining share of budget dedicated to housing when income increases, which is a robust empirical finding. In practice, this translates into increased residential segregation, as poor households struggle to meet their basic need in housing in expensive places.

16

Note however that the size of informal backyards and informal settlements is fixed according to the value of the shack_size parameter. The size of formal subsidized dwellings (excluding backyard) is also fixed by the RDP_size parameter.

17

See Galiani et al. [2017] for more details.

18

It could be that households renting out part of their backyard also provide the “shack” to live in. If we take the reasoning further, those households could even turn into mini-developers, providing structures of various sizes and materials for instance. Empirically, most of those structures are not concrete and have a rather standardized size, hence our simplifying assumptions. Also, we choose to have the dwellers pay for the structure as building costs for such non-durable housing are often closer to a flow cost of maintenance than to a sunk cost of construction (see for example Henderson et al. [2021]). Still, we could switch sides easily.

19

The alternative to the absentee landlord assumption is the public ownership assumption: in that case, all housing revenues are equally shared among residents of the city. The choice is supposed to reflect the ownership structure of the city, but in practice it has little impact on its spatial structure [Avner et al., 2022]. The main difference is that we do not consider the same notions of welfare in each case.

20

Note that, in this kind of static models where prices and rents are constant over time, it is equivalent to consider choices to buy or to rent, as price is just the capitalized value of all future rent flows. We will therefore focus on housing rents only, as is standard in the literature.

21

Note that in the benchmark case with no market failure, tax equivalence results hold that the burden of added maintenance costs (that we assimilate to a tax) is shared across supply and demand, not on the basis of which side the tax applies to, but depending on their relative elasticities [Auerbach, 2019]. Therefore, the structural assumptions made on the distribution of those costs should not have an impact on overall welfare.

22

Remember that households rent housing in the formal private and subsidized sectors, but direcly rent land in the informal backyard and settlement sectors.

23

This is based on the formula in Equilibrium housing supply: the value of \(\kappa\) is updated to offset the impact on \(s_{FP}(x)\) of any artifical increase in \(R_{FP}(x)\) due to inflation.

24

In the absence of quasi-natural experiments, for such estimated parameters to be properly identified in our simulations (even for a well-specified theoretical structure), we need to assume that the variables used in the calibration are close to a long-term equilibrium at the baseline year we study (no deviations due to the durability of housing, etc.). A good robustness check would be to see how our estimates would change when running the calibration over previous periods.

25

Although it is also a utility function parameter, the local disamenity index associated with informal settlements and backyards will be calibrated separately, from model inversion (see Ahlfeldt et al. [2015]). This is because we do not have access to the same kind of exogenous amenity data we use to calibrate the local amenity score directly.

26

We remind the reader that, conditional on some error term distribution, maximum likelihood estimation (MLE) consists in estimating parameters such as they maximize the probability that the posited statistical model indeed predicts the value of outcome variables. This probability is expressed as a likelihood function, which is log-linearized in practice for optimization purposes, hence our focus on log-likelihoods. Note that, contrary to MLE, OLS does not require any assumption on the error term distribution (but may be less efficient or misspecified in some cases).

27

We could also adopt simpler Cobb-Douglas preferences, and calibrate the parameters separately for each income group, as in Diamond and Gaubert [2022]. The problem with such approach is that it is not properly micro-founded: we assume that different households have different income elasticities where, in fact, they just differ in income levels. The Stone-Geary specification allows to recover the observed heterogeneous expenditure shares with a single elasticity parameter, by considering housing as a necessity good. It is not only of theoretical, but also practical importance: the expenditure shares will be allowed to adapt continuously with income levels, not just across discrete income groups. More generally, adding heterogeneity dimensions increases the risk of overfitting the model, threatening its external validity for counterfactuals. In fact, we could also heterogenize the gravity parameter \(\lambda\) and the amenity score \(A(x)\) with respect to income groups, as we expect them to have different mobilities and tastes: we only recommend doing so with a strong theoretical and empirical ground.

28

Note that the Cobb-Douglas specification used for the housing production function is also a particular case of a more general CES function with an elasticity of substitution equal to 1. The difference with Stone-Geary preferences is that, whereas Combes et al. [2021] do not reject a unit elasticity of substitution for housing production, Finlay and Williams [2022] do so for preferences. This is the reason why we are more confident with our structural estimation of housing production elasticities than utility function elasticities.

29

We could alternatively run a MLE (instead of OLS estimation) and directly store the associated maximum log-likelihood, but this is equivalent for normally distributed error terms of mean zero.